Equilibria in linear systems
It is common for linear systems to evolve towards a single fixed state.
The assumption that most dynamic systems have a single preferred fixed state for a given set of circumstances appears to be one of the drivers behind Central Bank policies. It is debatable whether the Central Banks recognize nonlinearities in socio-economic systems, or whether they do but are unable to express it it the typical 10-second soundbite that the average consumer of their "products" can absorb.
Certainly, the common example of using lower interest rates to combat unemployment sounds like the kind of thinking one expects about a system with a single equilibrium state. The notion that low interest rates ultimately lead to higher inflation reflects similar thinking.
Here are some examples in phase space of single equilibria in a simple linear system.
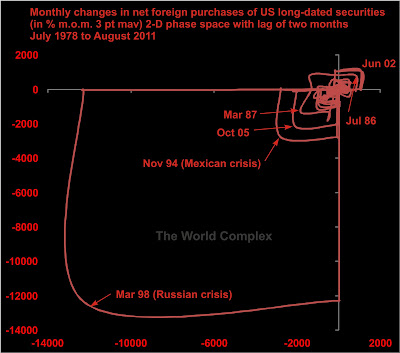
When all trajectories within a given region of phase space gradually and continually converge towards a single point, then the equilibrium can be described as being asymptotically stable, and is commonly referred to as a point attractor. Note that even though trajectories 1 and 3 appear to cross, they actually do not as one passes over the other in a three- (or higher-) dimensional projection.
Line crossings in a properly "unfolded" phase space portrait cannot cross, as each uniquely defined state represents a unique value and a unique sequence of values of the higher time derivatives of the time series from which they are projected. If two trajectories converged onto a single point, it would be impossible for them to diverge again--hence no crossings. If there appear to be crossings in a reconstructed phase space, then the phase space needs to be projected in more dimensions. Unfortunately, there are logistical problems with presenting even three (let alone more) dimensional figures, which is why I have limited the figures presented to two dimensions, with a caveat that apparent crossings mean we should really be looking at a projection in at least three dimensions.
Often we find that rather than continuous convergence, two states which originate close to one another as well as to a particular point in phase space tend to stay close together and near to the point. Such stability is called Lyapunov stability (sometimes a Lyapunov-stable area, or LSA). More formally, we might state that all states with a region of phase space (a) will tend to remain in another (possibly smaller) region of phase space (b). Once again, note that the apparent crossing of trajectories only suggests that we should construct this phase space in at least three dimensions.
Another form of equilibrium is the limit cycle. It represents a form of asymptotic stability whereby the final equilibrium is not a point but a continuous cycle. There is no reason that the cycle needs to form an ellipse--any closed shape is possible. In higher-dimensional projections, a limit cycle may be in the form of a shell, or a torus.
Equilibria in chaotic systems
A different form of equilibrium was discovered by Edward Lorenz in 1963. A system defined by three nonlinear differential equations reached a complex equilibrium in which any state evolved continually towards the "attractor"; however any two states starting arbitrarily close would diverge exponentially, even though at the same time they would both evolve in similar fashion through phase space.
This form of attractor was called a "strange attractor". Although it occupies a finite volume of phase space, the trajectory from any arbitrary point would evolve in unique fashion, so that all evolving trajectories from any arbitrary starting point would appear similar, yet would occupy subtly different regions of phase space.
Multiple equilibria (multistability)
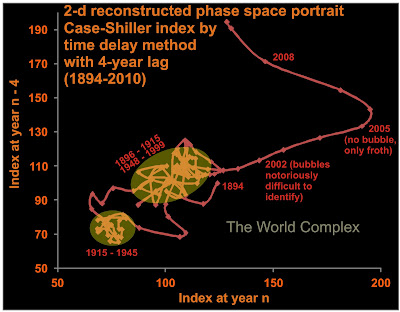
In some complex systems, we observe any number of disjoint Lyapunov-stable areas (LSA), each separated in phase space by a separatrix [Kauffman, 1993]. At any given time, the state of the system occupies only one such LSA, so that their number therefore constitutes the total number of alternative long-term behaviors, or equilibrium states, of the system. Since an LSA is likely to be smaller than the total allowable range of states, the system tends to become boxed into an LSA unless it is subjected to external forcing. When the state approaches a separatrix, small perturbations can trigger a change to a nearby state (a bifurcation), resulting in chaotic changes in the evolution of the system [Parker and Chua, 1989]. Thus very complex behavior can arise in multistable systems.
Multistable behaviour generally arises from systems in which feedbacks, both negative and positive, impact a system which is perturbed by some sort of external forcing. Negative feedback tends to resist external forcing, resulting in stability in some regions of phase space. If the external forcing is sufficient to overcome the feedback, then positive feedback may actually accelerate the changes, causing the state to evolve rapidly towards another area of stability.
The smooth variation of one or more parameters in the system may result in a change in the type of or the number of attractors in the system, or even in the order in which the attractors are visited. Such a response is called a bifurcation. Bifurcations can represent a sudden transition within a system characterized by purely chaotic attractors to one with one or more LSA; between one LSA and multiple LSA; or between different configurations of LSA.
Bifurcations represent changes in the organization of the system, and their existence has been suggested by models [e.g., Ghil, 1994; Rahmstorf, 1995], and more rarely from observations [Livina et al., 2010; discussed here] in future installments we will demonstrate such behaviour in natural systems. Initially, however, we will concentrate on interpretation of some of the phase space portraits presented last time.
References
Ghil, M. (1994), Cryothermodynamics: the chaotic dynamics of paleoclimate, Physica, 77D: 130-159.
Kauffman, S. (1993), The Origins of Order: Self-Organization and Selection in Evolution, Oxford Univ. Press, New York, 734 p.
Livina, V. N., Kwasniok, F., and Lenton, T. M. (2010), Potential analysis reveals changing number of climate states during the last 60 kyr. Climate of the Past, 6, 77-82, doi: 10.5194/cp-6-77-2010.
Parker, T. S. and L. O. Chua, (1989), Practical Numerical Algorithms for Chaotic Systems, Springer-Verlag, New York.
Rahmstorf, S. (1995), Bifurcation of the Atlantic thermohaline circulation in response to changes in the hydrologic cycle. Nature, 378, 145-149.
It is common for linear systems to evolve towards a single fixed state.
The assumption that most dynamic systems have a single preferred fixed state for a given set of circumstances appears to be one of the drivers behind Central Bank policies. It is debatable whether the Central Banks recognize nonlinearities in socio-economic systems, or whether they do but are unable to express it it the typical 10-second soundbite that the average consumer of their "products" can absorb.
Certainly, the common example of using lower interest rates to combat unemployment sounds like the kind of thinking one expects about a system with a single equilibrium state. The notion that low interest rates ultimately lead to higher inflation reflects similar thinking.
Here are some examples in phase space of single equilibria in a simple linear system.
When all trajectories within a given region of phase space gradually and continually converge towards a single point, then the equilibrium can be described as being asymptotically stable, and is commonly referred to as a point attractor. Note that even though trajectories 1 and 3 appear to cross, they actually do not as one passes over the other in a three- (or higher-) dimensional projection.
Line crossings in a properly "unfolded" phase space portrait cannot cross, as each uniquely defined state represents a unique value and a unique sequence of values of the higher time derivatives of the time series from which they are projected. If two trajectories converged onto a single point, it would be impossible for them to diverge again--hence no crossings. If there appear to be crossings in a reconstructed phase space, then the phase space needs to be projected in more dimensions. Unfortunately, there are logistical problems with presenting even three (let alone more) dimensional figures, which is why I have limited the figures presented to two dimensions, with a caveat that apparent crossings mean we should really be looking at a projection in at least three dimensions.
Often we find that rather than continuous convergence, two states which originate close to one another as well as to a particular point in phase space tend to stay close together and near to the point. Such stability is called Lyapunov stability (sometimes a Lyapunov-stable area, or LSA). More formally, we might state that all states with a region of phase space (a) will tend to remain in another (possibly smaller) region of phase space (b). Once again, note that the apparent crossing of trajectories only suggests that we should construct this phase space in at least three dimensions.
Another form of equilibrium is the limit cycle. It represents a form of asymptotic stability whereby the final equilibrium is not a point but a continuous cycle. There is no reason that the cycle needs to form an ellipse--any closed shape is possible. In higher-dimensional projections, a limit cycle may be in the form of a shell, or a torus.
Equilibria in chaotic systems
A different form of equilibrium was discovered by Edward Lorenz in 1963. A system defined by three nonlinear differential equations reached a complex equilibrium in which any state evolved continually towards the "attractor"; however any two states starting arbitrarily close would diverge exponentially, even though at the same time they would both evolve in similar fashion through phase space.
This form of attractor was called a "strange attractor". Although it occupies a finite volume of phase space, the trajectory from any arbitrary point would evolve in unique fashion, so that all evolving trajectories from any arbitrary starting point would appear similar, yet would occupy subtly different regions of phase space.
Multiple equilibria (multistability)
In some complex systems, we observe any number of disjoint Lyapunov-stable areas (LSA), each separated in phase space by a separatrix [Kauffman, 1993]. At any given time, the state of the system occupies only one such LSA, so that their number therefore constitutes the total number of alternative long-term behaviors, or equilibrium states, of the system. Since an LSA is likely to be smaller than the total allowable range of states, the system tends to become boxed into an LSA unless it is subjected to external forcing. When the state approaches a separatrix, small perturbations can trigger a change to a nearby state (a bifurcation), resulting in chaotic changes in the evolution of the system [Parker and Chua, 1989]. Thus very complex behavior can arise in multistable systems.
Multistable behaviour generally arises from systems in which feedbacks, both negative and positive, impact a system which is perturbed by some sort of external forcing. Negative feedback tends to resist external forcing, resulting in stability in some regions of phase space. If the external forcing is sufficient to overcome the feedback, then positive feedback may actually accelerate the changes, causing the state to evolve rapidly towards another area of stability.
The smooth variation of one or more parameters in the system may result in a change in the type of or the number of attractors in the system, or even in the order in which the attractors are visited. Such a response is called a bifurcation. Bifurcations can represent a sudden transition within a system characterized by purely chaotic attractors to one with one or more LSA; between one LSA and multiple LSA; or between different configurations of LSA.
Bifurcations represent changes in the organization of the system, and their existence has been suggested by models [e.g., Ghil, 1994; Rahmstorf, 1995], and more rarely from observations [Livina et al., 2010; discussed here] in future installments we will demonstrate such behaviour in natural systems. Initially, however, we will concentrate on interpretation of some of the phase space portraits presented last time.
References
Ghil, M. (1994), Cryothermodynamics: the chaotic dynamics of paleoclimate, Physica, 77D: 130-159.
Kauffman, S. (1993), The Origins of Order: Self-Organization and Selection in Evolution, Oxford Univ. Press, New York, 734 p.
Livina, V. N., Kwasniok, F., and Lenton, T. M. (2010), Potential analysis reveals changing number of climate states during the last 60 kyr. Climate of the Past, 6, 77-82, doi: 10.5194/cp-6-77-2010.
Parker, T. S. and L. O. Chua, (1989), Practical Numerical Algorithms for Chaotic Systems, Springer-Verlag, New York.
Rahmstorf, S. (1995), Bifurcation of the Atlantic thermohaline circulation in response to changes in the hydrologic cycle. Nature, 378, 145-149.